What is Quantum Computing & How Does it Work?

Technology giants like Google, IBM, Amazon, and Microsoft are pouring resources into quantum computing. The goal of quantum computing is to create the next generation of computers and overcome classic computing limits.

Despite the progress, there are still unknown areas in this emerging field.

This article is an introduction to the basic concepts of quantum computing. You will learn what quantum computing is and how it works, as well as what sets a quantum device apart from a standard machine.

What is Quantum Computing? Defined

Quantum computing is a new generation of computers based on quantum mechanics, a physics branch that studies atomic and subatomic particles. These supercomputers perform computations at speeds and levels an ordinary computer cannot handle.

These are the main differences between a quantum device and a regular desktop:

• Different architecture: Quantum computers have a different architecture than conventional devices. For example, instead of traditional silicon-based memories or processors, different technology platforms, such as super conducting circuits and trapped atomic ions are utilized.
• Computational intensive use cases: A casual user might not have much use for a quantum computer. The computational-heavy focus and complexity of these machines make them suitable for corporate and scientific settings in the foreseeable future.

Unlike a standard computer, its quantum counterpart can perform multiple operations simultaneously. These machines also store more states per unit of data and operate on more efficient algorithms.

Incredible processing power makes quantum computers capable of solving complex tasks and searching through unsorted data.

What is Quantum Computing Used for? Industry Use Cases

The adoption of more powerful computers benefits every industry. However, some areas already stand out as excellent opportunities for quantum computers to make a mark:

• Healthcare: Quantum computers help develop new drugs at a faster pace. DNA research also benefits greatly from using quantum computing.
• Cybersecurity: Quantum programming can advance data encryption. The new Quantum Key Distribution (QKD) system, for example, uses light signals to detect cyber attacks or network intruders.
• Finance: Companies can optimize their investment portfolios with quantum computers. Improvements in fraud detection and simulation systems are also likely.
• Transport: Quantum computers can lead to progress in traffic planning systems and route optimization.

What are Qubits?

The key behind a quantum computer’s power is its ability to create and manipulate quantum bits, or qubits.

Here is the state of a qubit q₀:

q0 = a|0> + b|1>, where a2 + b2 = 1

The likelihood of q₀ being 0 when measured is a². The probability of it being 1 when measured is b². Due to the probabilistic nature, a qubit can be both 0 and 1 at the same time.

For a qubit q₀ where a = 1 and b = 0, q₀ is equivalent to a classical bit of 0. There is a 100% chance to get to a value of 0 when measured. If a = 0 and b = 1, then q₀ is equivalent to a classical bit of 1. Thus, the classical binary bits of 0 and 1 are a subset of qubits.

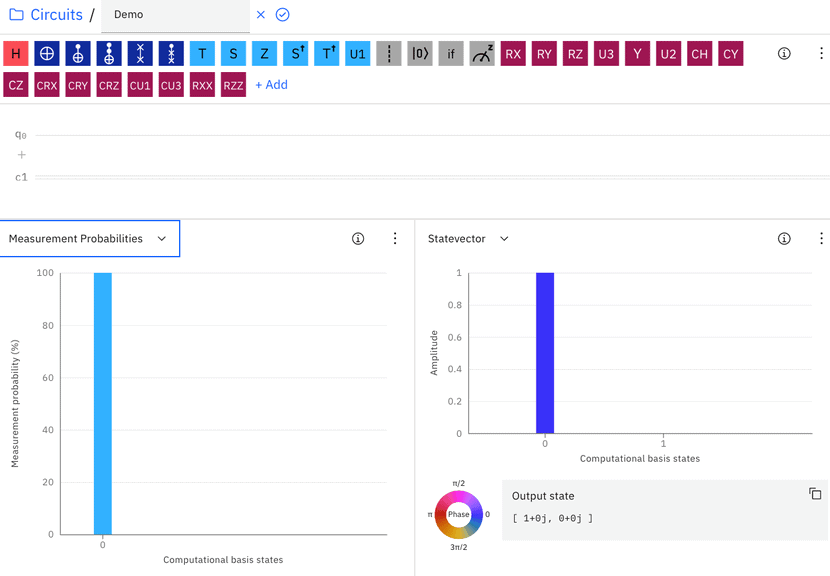
Now, let’s look at an empty circuit in the IBM Circuit Composer with a single qubit q₀ (Figure 1). The “Measurement probabilities” graph shows that the q₀ has 100% of being measured as 0. The “Statevector” graph shows the values of a and b, which correspond to the 0 and 1 “computational basis states” column, respectively.

In the case of Figure 1, a is equal to 1 and b to 0. So, q₀ has a probability of 1² = 1 to be measured as 0.

A connected group of qubits provides more processing power than the same number of binary bits. The difference in processing is due to two quantum properties: superposition and entanglement.

Superposition in Quantum Computing

When 0 < a and b < 1, the qubit is in a so-called superposition state. In this state, it is possible to jump to either 0 or 1 when measured. The probability of getting to 0 or 1 is defined by a² and b².

The Hadamard Gate is the basic gate in quantum computing. The Hadamard Gate moves the qubit from a non-superposition state of 0 or 1 into a superposition state. While in a superposition state, there is a 0.5 probability of it being measured as 0. There is also a 0.5 chance of the qubit ending up as 1.

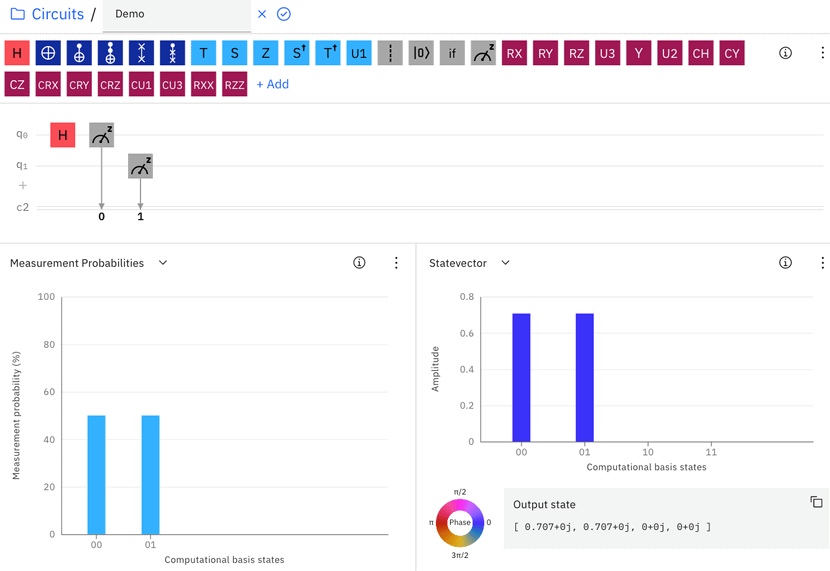
Let’s look at the effect of adding the Hadamard Gate (shown as a red H) on q₀ where q₀ is currently in a non-superposition state of 0 (Figure 2). After passing the Hadamard gate, the “Measurement Probabilities” graph shows that there is a 50% chance of getting a 0 or 1 when q₀ is measured.

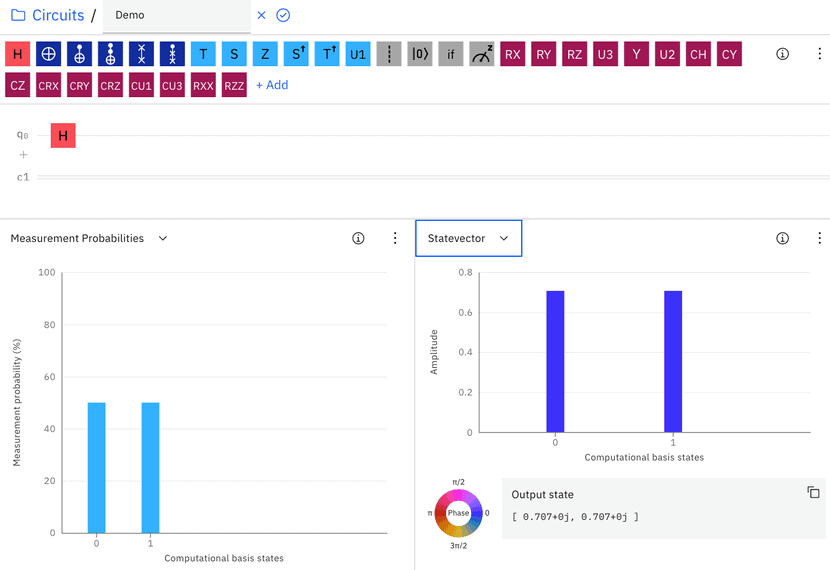
The “Statevector” graph shows the value of a and b, which are both square roots of 0.5 = 0.707. The probability for the qubit to be measured to 0 and 1 is 0.707² = 0.5, so q₀ is now in a superposition state.

What Are Measurements?

When we measure a qubit in a superposition state, the qubit jumps to a non-superposition state. A measurement changes the qubit and forces it out of superposition to the state of either 0 or 1.

If a qubit is in a non-superposition state of 0 or 1, measuring it will not change anything. In that case, the qubit is already in a state of 100% being 0 or 1 when measured.

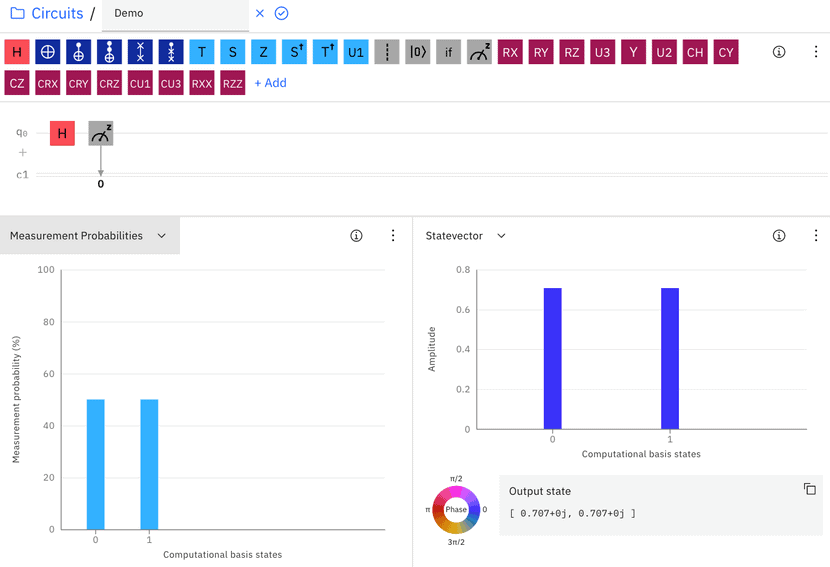
Let us add a measurement operation into the circuit (Figure 3). We measure q₀ after the Hadamard gate and output the value of the measurement to bit 0 (a classical bit) in c1:

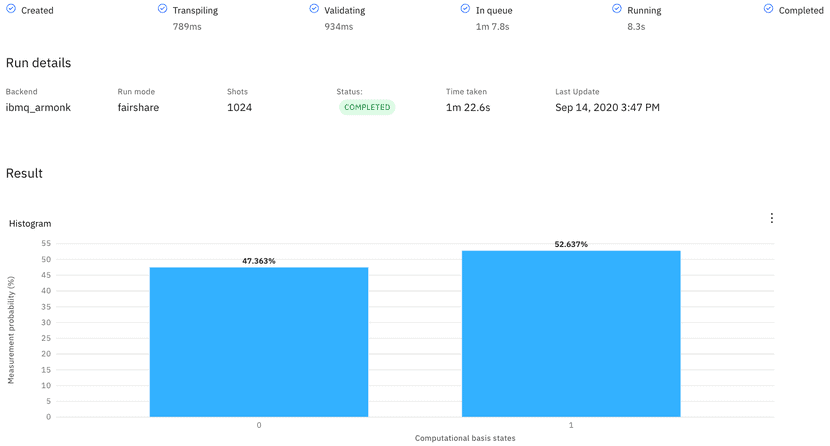
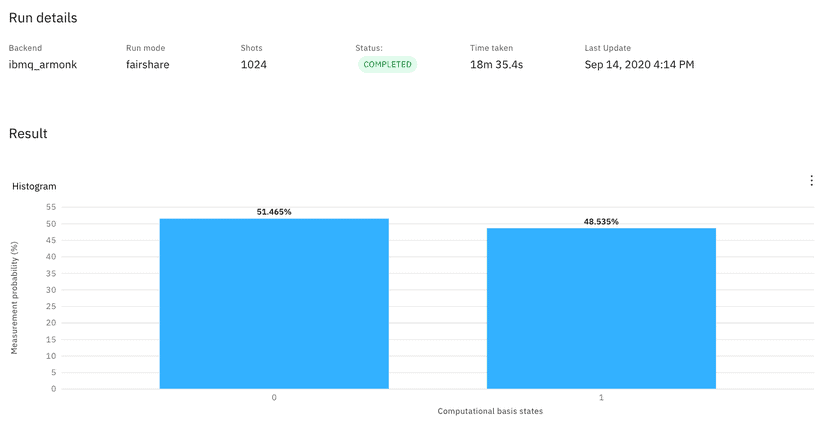
To see the results of the q₀ measurement after the Hadamard Gate, we send the circuit to run on an actual quantum computer called “ibmq_armonk.” By default, there are 1024 runs of the quantum circuit. The result (Figure 4) shows that about 47.4% of the time, the q₀ measurement is 0. The other 52.6% of times, it is measured as 1:

The second run (Figure 5) yields a different distribution of 0 and 1, but still close to the expected 50/50 split:

Entanglement in Quantum Computing

If two qubits are in an entanglement state, the measurement of one qubit instantly “collapses” the value of the other. The same effect happens even if the two entangled qubits are far apart.

Let us look at an example. A quantum operation that puts two untangled qubits into an entangled state is the CNOT gate. To demonstrate this, we first add another qubit q₁, which is initialized to 0 by default. Before the CNOT gate, the two qubits are untangled, so q₀ has a 0.5 chance of being 0 or 1 due to the Hadamard gate, while q₁ is going to be 0. The “Measurement Probabilities” graph (Figure 6) shows that the probability of (q₁, q₀) being (0, 0) or (0, 1) is 50%:

Then we add the CNOT gate (shown as a blue dot and the plus sign) that takes the output of q₀ from the Hadamard gate and q₁ as inputs. The “Measurement Probabilities” graph now shows that there is a 50% chance of (q₁, q₀) being (0, 0) and 50% of being (1, 1) when measured (Figure 7):

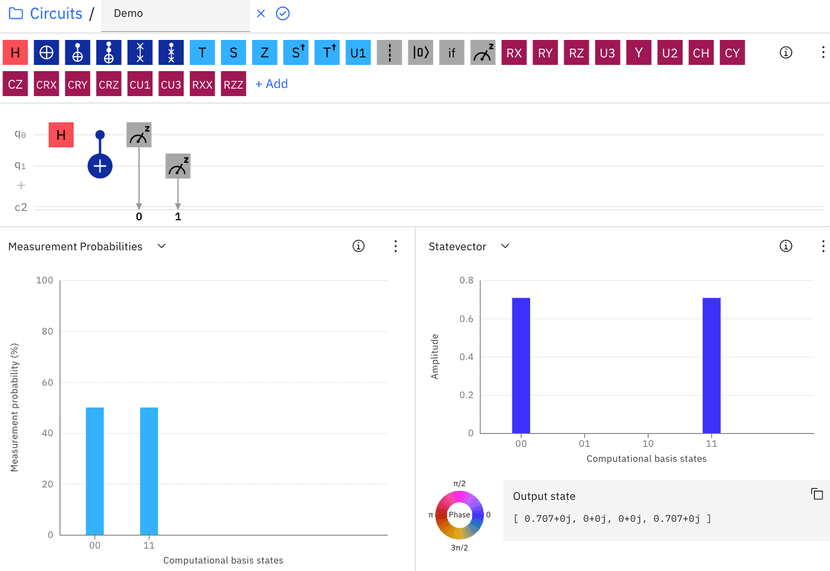
There is zero chance of getting (0, 1) or (1, 0). Once we determine the value of one qubit, we know the other’s value because the two must be equal. In such a state, q₀ and q₁ are entangled.

Let us run this on an actual quantum computer and see what happens (Figure 8):

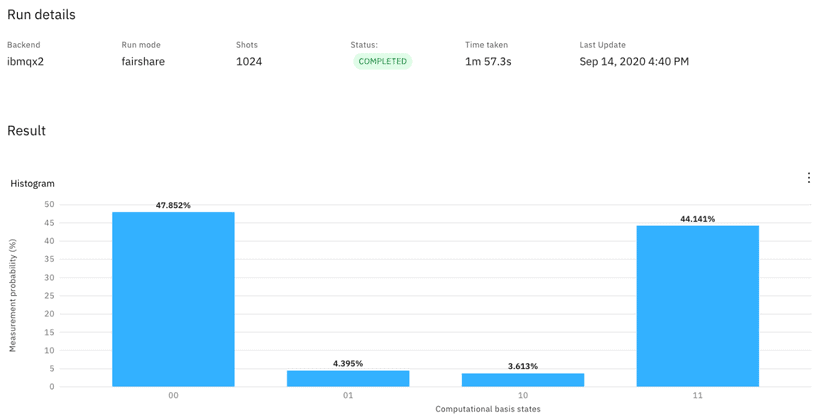
We are close to a 50/50 distribution between the ‘00’ and ‘11’ states. We also see unexpected occurrences of ‘01’ and ‘10’ due to the quantum computer’s high error rates. While error rates for classical computers are almost non-existent, high error rates are the main challenge of quantum computing.

The Bell Circuit is Only a Starting Point

The circuit shown in the ‘Entanglement’ section is called the Bell Circuit. Even though it is basic, that circuit shows a few fundamental concepts and properties of quantum computing, namely qubits, superposition, entanglement, and measurements. The Bell Circuit is often cited as the Hello World program for quantum computing.

By now, you probably have many questions, such as:

• How do we physically represent the superposition state of a qubit?
• How do we physically measure a qubit, and why would that force a qubit into 0 or 1?
• What exactly is the |0> and |1> in the formulation of qubit?
• Why do a² and b² correspond to the chance of a qubit being measured as 0 and 1?
• What are the mathematical representations of the Hadamard and CNOT gates? Why do gates put qubits into superposition and entanglement states?
• Can we explain the phenomenon of entanglement?

There are no shortcuts to learning quantum computing. The field touches on complex topics spanning physics, mathematics, and computer science.

There is an abundance of good books and video tutorials that introduce the technology. These resources typically cover pre-requisite concepts like linear algebra, quantum mechanics, and binary computing.

In addition to books and tutorials, you can also learn a lot from code examples. Solutions to financial portfolio optimization and vehicle routing, for example, are great starting points for learning about quantum computing.

The Next Step in Computer Evolution

Quantum computers have the potential to exceed even the most advanced supercomputers. Quantum computing can lead to breakthroughs in science, medicine, machine learning, construction, transport, finances, and emergency services.

The promise is apparent, but the technology is still far from being applicable to real-life scenarios. New advances emerge every day, though, so expect quantum computing to cause significant disruptions in years to come.